Simulating a Fitness Trait


  The parameter file below illustrates how to simulate a fitness trait only. When simulating a fitness trait it is important to ensure that you have enough founder individuals because a portion will not make it to breeding age. Therefore, an extra 140 males and 200 females were added to the founder population to ensure enough individuals are available to generate the breeding population. This will also impact the replacement rate because if enough progeny aren't available to remain at the chosen male and female population size the simulation will exit. A full description of how the fitness value of an individual impacts its ability to make it to breeding age is described in the "QTL/FTL Distribution Parameters" link.

−−−−−−−| Simulating a Fitness Trait |−−−−−−−
−| General |−
START: sequence
SEED: 1500
−| Genome & Marker |−
CHR: 3
CHR_LENGTH: 150 150 150
NUM_MARK: 4000 4000 4000
QTL: 0 0 0
FIT_LETHAL: 50 50 50
FIT_SUBLETHAL: 50 50 50
−| Population |−
FOUNDER_Effective_Size: 250
MALE_FEMALE_FOUNDER: 150 600 random 0
VARIANCE_A: 0.0
−| Selection |−
GENERATIONS: 25
INDIVIDUALS: 10 0.2 400 0.2
PROGENY: 1
SELECTION: random high
CULLING: random 10
-| Mating |-
MATING: random
-| OUTPUT OPTIONS |-
GENOTYPES: no

Parameter File Summary
  Sequence information is generated for three chromosomes with a length of 150 Megabases. The genome simulated has a low degree of short-range LD (250). The SNP panel contains 12,000 marker (i.e. 4,000 markers per chromosome). For each chromosome, 50 lethal and 50 sub-lethal mutations were generated. The quantitative trait has a broad sense heritability of 0.0 and therefore an animals phenotype is only a function of random environmental deviations with a variance of 1.0. The founder population consisted of 150 males and 600 females. For each generation, a total of 10 males and 400 females are in the population. A total of 10 and 80 (0.2 replacement rate) male and female parents, respectively, are culled and replaced by new progeny each generation. Across all generations animals are randomly selected or culled each generation. The maximum number of generations an animal can remain in the breeding population is 10. Each mating pair produced one progeny and parents were mated at random. The genotypes are not saved to a file.

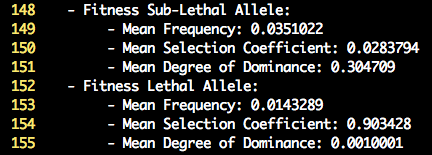
  Inspection of the log file will provide summary statistics on the mean selection coefficients and degree of dominance for the lethal and sub-lethal fitness effect along with their associated frequency. The default settings for the lethal mutations result in a high selection coefficient (0.90) and very little dominance (0.001). Therefore the heterozygote is normal, while the unfavorable homozygote has a low fitness value. The settings for the sub-lethal mutations result in a lower selection coefficient (0.03) and moderate degree of dominance (0.30). Therefore the heterozygote now has a reduced fitness value compared to the fittest homozygote. Lastly, the mean allele frequency of the unfavorable allele is higher for sub-lethal compared to lethals. Below is a screenshot of the lines in the log file that display the summary statistics.

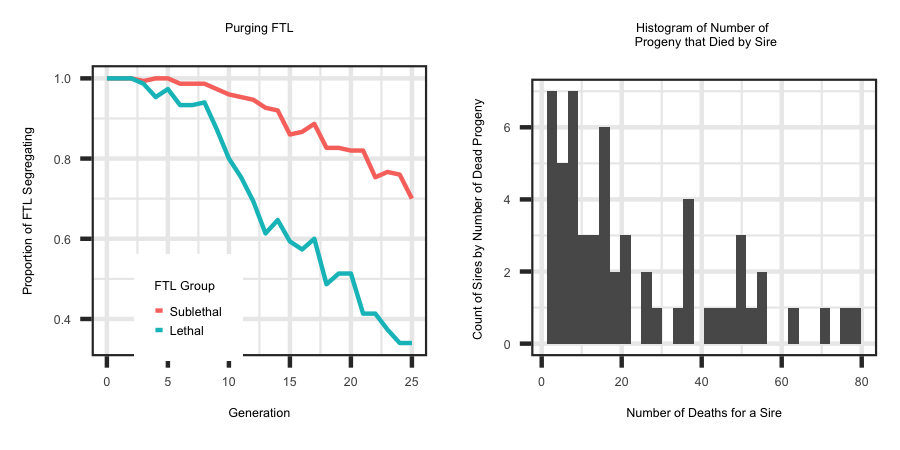
  When a fitness trait is simulated, the animals that died due to fitness are placed in the "Low_Fitness" along with summary statistics for the respective animals. Utilizing the R code outlined below the following plots were generated to illustrate the type of information in the "Low_Fitness" file.

R-Code
rm(list=ls()); gc()
library(ggplot2); library(tidyverse)
## Change
setwd("/Users/jeremyhoward/Desktop/C++Code/18_GenoDiver_V3/GenoDiverFiles/")
##############################################
## Number of FTL Purged by Fitness Group ##
##############################################
df <- read_table2(file="QTL_new_old_Class",col_names = TRUE,col_type = "dcccccc")
## split apart frequencies ##
freq <- matrix(unlist(strsplit(df$Freq, "_")), ncol = 26, byrow = TRUE)
freq <- apply(freq, 2, as.numeric)
## y axis is in terms of change in allele frequency of unfavorable allele ##
## if greater than 0.5 at generation 0 then take 1 - freq ##
X <- which(freq[,1] > 0.50)
freq[X, ] <- 1 - freq[X, ]
## If purged set to 0 else set to 1 #
freq <- ifelse(freq == 0.0, 0,1)
## Do Sublethals ##
X <- which(df$Type == 5)
plotdf <- data.frame(Generation = c(0:25),
  PropSegregating = colSums(freq[X, ]) / length(X),
  Group = c(rep("Sublethal",26)))
## Do Lethals ##
X <- which(df$Type == 4)
plotdfa <- data.frame(Generation = c(0:25),
  PropSegregating = colSums(freq[X, ]) / length(X),
  Group = c(rep("Lethal",26)))
plotdf <- rbind(plotdf,plotdfa); rm(X,plotdfa)

ggplot(plotdf, aes(x = Generation, y = PropSegregating,group=Group, colour = Group)) + geom_line() + theme_bw() +
  labs(title = "Purging FTL", x = "Generation", y = "Proportion of FTL Segregating") +
  scale_colour_discrete(name ="FTL Group") + theme(plot.title = element_text(hjust = 0.5), legend.position="bottom")
##############################################################
### Grab All Unique Sires and Plot Number of deaths by Sire ##
##############################################################
df <- read_table2(file="Low_Fitness",col_names = TRUE,col_type = "iiiddddiiiiddcddd")
## Get death counts by sire ##
SireDeath <- aggregate(TGV ~ Sire, data=df,FUN=length) # get count by sire
SireDeath <- SireDeath[which(SireDeath$Sire != 0), ] # remove unknown sire groups
SireDeath <- SireDeath[order(-SireDeath$TGV), ] # order largest to smallest

ggplot(data=SireDeath, aes(SireDeath$TGV)) + geom_histogram() + theme_bw() +
  ylab ("Count of Sires by Number of Dead Progeny ") + xlab ("Number of Deaths for a Sire") + theme_bw()+
  ggtitle("Histogram of Number of \n Progeny that Died by Sire") + theme(plot.title = element_text(hjust = 0.5))