Simulating a Fitness and Quantitative Trait


  The parameter file outlined below illustrates how to simulate a quantitative trait that has a proportion (i.e. 50%) of the quantitative trait loci (QTL) also having a fitness effect. The relationship between the QTL with a fitness effect has a positive correlation of 0.20, but the two traits are antagonistic based on the way the fitness value of a loci is parameterized. High selection coefficients (s) result in the unfavorable homozygote genotype to be less fit and is described in detail in the 'QTL/FTL Distributions' link. As outlined in the previous example, it is important to add a few extra animals in the founder population since a portion will die. If the number of male or female founder animals is smaller than the population size it will exit out of the program. Therefore, careful consideration of the number and magnitude of fitness effects along with the number of progeny produced per mating pair needs to be carefully considered when constructing the simulation design.

−−−−−−−| Quantitative and Fitness Trait |−−−−−−−
−| General |−
START: sequence
SEED: 1501
−| Genome & Marker |−
CHR: 3
CHR_LENGTH: 150 150 150
NUM_MARK: 4000 4000 4000
QTL: 150 150 150
FIT_LETHAL: 15 15 15
FIT_SUBLETHAL: 100 100 100
−| Population |−
FOUNDER_Effective_Size: Ne70
MALE_FEMALE_FOUNDER: 100 400 random 3
VARIANCE_A: 0.20
VARIANCE_D: 0.05
COVAR: 0.5 0.2
−| Selection |−
GENERATIONS: 20
INDIVIDUALS: 50 0.2 250 0.2
PROGENY: 1
SELECTION: ebv high
EBV_METHOD: pblup
CULLING: ebv 5
-| Mating |-
MATING: random

Parameter File Summary
  Sequence information is generated for three chromosomes with a length of 150 Megabases (Mb). The simulated genome has a high degree of short-range LD (Ne70). The SNP panel contains 12,000 markers (i.e. 4,000 markers per chromosome). For each chromosome, 150 randomly placed QTL were generated. Also, 15 lethal and 100 sub-lethal mutations were generated for each chromosome. The narrow and broad sense heritability for the quantitative trait is 0.20 and 0.25, respectively. The phenotypic variance is by default set at 1.0, and therefore the residual variance is 0.75. Half of the QTL also have a fitness effect and the correlation between the additive QTL effects and sub-lethal selection coefficients is 0.20. The founder population consisted of 100 males and 400 females prior to determining whether an animals survived to breeding age. For each generation, a total of 50 males and 250 females are in the population. Random selecton of progeny and culling of parents was conducted for 3 generations in order to build up the pedigree. A total of 10 and 50 (0.2 replacement rate) male and female parents, respectively, are culled and replaced by new progeny each generation. After 3 generations, animals with a high EBV were selected or culled each generation. Twenty generations are simulated.The EBV are estimated using an animal model with a pedigree-based relationship matrix. Each mating pair produced one progeny. Parents were mated at random.

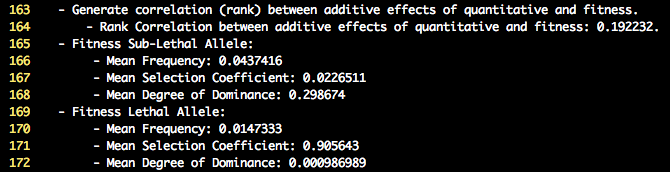
  Inspection of the log file will provide summary statistics on the mean selection coefficients and degree of dominance for the lethal and sub-lethal fitness effect along with their associated frequency. The default settings for the lethal mutations result in a high selection coefficient (0.90) and very little dominance (0.001). Therefore the heterozygote is normal, while the unfavorable homozygote has a low fitness value. The settings for the sub-lethal mutations result in a lower selection coefficient (0.02) and moderate degree of dominance (0.30). Therefore the heterozygote now has a reduced fitness value compared to the fittest homozygote. Lastly, the mean allele frequency of the unfavorable allele is higher for sub-lethal compared to lethals. Below is a screenshot of the lines in the log file that display the summary statistics.

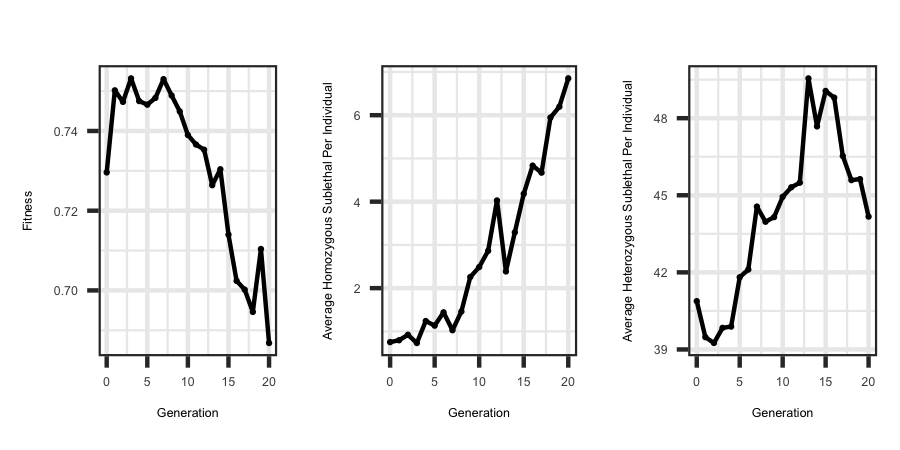
  Utilizing the R code outlined below the following plots were generated from the output files.


R-Code
rm(list=ls()); gc()
library(ggplot2); library(tidyverse)
## Change
setwd("/Users/jeremyhoward/Desktop/C++Code/18_GenoDiver_V3/GenoDiverFiles/")
########################################################################################################
## Plot Mean Fitness, Average Homozygous and Heterozygous Sublethal per Individual Across Generations ##
########################################################################################################
df <- read_table2(file="Summary_Statistics_DataFrame_Inbreeding",col_names = TRUE,col_type = "dcccccccccccccc") %>%
  mutate(fitness = as.numeric(matrix(unlist(strsplit(fitness, "[()]")), ncol = 2, byrow = TRUE)[, 1]),
               homosublethal = as.numeric(matrix(unlist(strsplit(homozysublethal, "[()]")), ncol = 2, byrow = TRUE)[, 1]),
               hetezsublethal = as.numeric(matrix(unlist(strsplit(hetezsublethal, "[()]")), ncol = 2, byrow = TRUE)[, 1])) %>%
  select(Generation,fitness,homosublethal,hetezsublethal)

ggplot(df, aes(x=Generation, y = fitness)) + geom_point(size = 3) + geom_line()
  labs(title = "", x = "Generation", y = "Fitness") + theme_bw() +

ggplot(df, aes(x=Generation, y = homosublethal)) + geom_point(size = 3) + geom_line()
  labs(title = "", x = "Generation", y = "Average Homozygous Sublethal Per Individual") + theme_bw() +

ggplot(df, aes(x=Generation, y = hetezsublethal)) + geom_point(size = 3) + geom_line()
  labs(title = "", x = "Generation", y = "Average Heterozygous Sublethal Per Individual") + theme_bw()