Phenotypic Selection and Culling


  The parameter file outlined below illustrates how to simulate a population undergoing selection and culling based on their phenotype. The sequence information generated from Example 1 was available, therefore the 'START' parameter is now founder. Furthermore, the same seed was utilized therefore the first 3 generations should be the same as in Examples 1 through 4 and after that changes occur due to a different selection criteria being utilized.

−−−−−−−| Running the Program Example |−−−−−−−
−| General |−
START: founder
SEED: 1500
−| Genome & Marker |−
CHR: 3
CHR_LENGTH: 150 150 150
NUM_MARK: 4000 4000 4000
QTL: 150 150 150
−| Population |−
FOUNDER_Effective_Size: Ne70
MALE_FEMALE_FOUNDER: 50 400 random 3
VARIANCE_A: 0.10
−| Selection |−
GENERATIONS: 15
INDIVIDUALS: 50 0.2 400 0.2
PROGENY: 1
SELECTION: phenotype high
CULLING: phenotype 5
-| Mating |-
MATING: random125 simu_anneal

Parameter File Summary
  Sequence information is generated for three chromosomes with a length of 150 Megabases (Mb). The simulated genome has a high degree of short-range LD (Ne70). The SNP panel contains 12,000 markers (i.e. 4,000 markers per chromosome). For each chromosome, 150 randomly placed QTL and zero FTL mutations were generated. The quantitative trait simulated has a narrow sense heritability of 0.10 and only additive effects are generated (i.e. no dominance). The phenotypic variance is by default set at 1.0, and therefore the residual variance is 0.90. The founder population consisted of 50 males and 400 females. For each generation, a total of 50 males and 400 females are in the population. Random selecton of progeny and culling of parents was conducted for 3 generations in order to build up the pedigree. A total of 10 and 80 (0.2 replacement rate) male and female parents, respectively, are culled and replaced by new progeny each generation. After 3 generations, animals with a high phenotype were selected or culled each generation. Fifteen generations were simulated. Each mating pair produced one progeny. Parents that had pedigree-based relationships greater than 0.125 were avoided, and this was optimized based on the simulated annealing method.

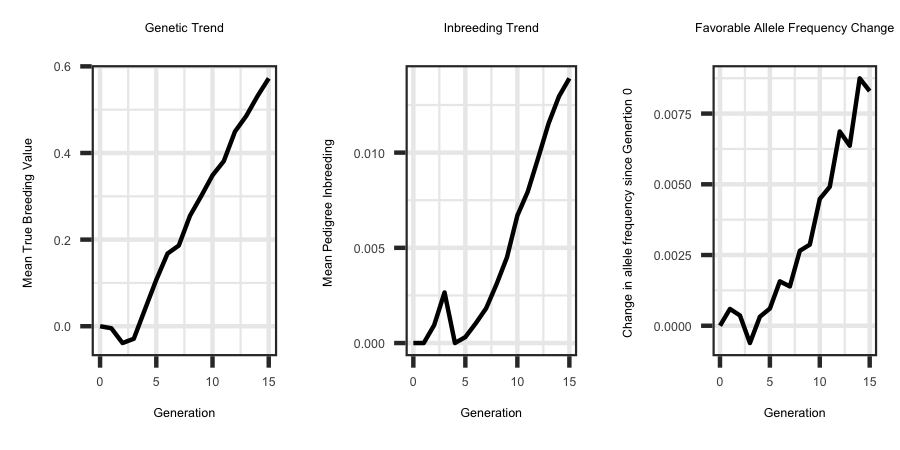
  Utilizing the R code outlined below the following plots were generated from the output files.

R-Code
rm(list = ls()); gc()
library(ggplot2); library(tidyverse)
## Change
setwd("/Users/jeremyhoward/Desktop/C++Code/18_GenoDiver_V3/GenoDiverFiles/")
#############################
## Plot True Genetic Value ##
#############################
df <- read_table2(file="Summary_Statistics_DataFrame_Performance",col_names = TRUE,col_type = "dcccccc") %>%
  mutate(.,tbv = as.numeric(matrix(unlist(strsplit(tbv, "[()]")), ncol = 2, byrow = TRUE)[, 1])) %>%
  select(Generation,tbv)

ggplot(df, aes(x = Generation, y = tbv)) + geom_line(size = 1) + ggtitle("Genetic Trend") + theme_bw() +
  theme(plot.title = element_text(hjust = 0.5)) + ylab("Mean True Breeding Value ")
##############################
## Plot Pedigree Inbreeding ##
##############################
df <- read_table2(file="Summary_Statistics_DataFrame_Inbreeding",col_names = TRUE,col_type = "dcccccccccccccc") %>%
  mutate(.,ped_f = as.numeric(matrix(unlist(strsplit(ped_f, "[()]")), ncol = 2, byrow = TRUE)[, 1])) %>%
  select(Generation,ped_f)

ggplot(df, aes(x = Generation, y = ped_f)) + geom_line(size = 1) + ggtitle("Inbreeding Trend") + theme_bw() +
  theme(plot.title = element_text(hjust = 0.5)) + ylab("Mean Pedigree Inbreeding ") + xlab("Generation")
#############################
## Allele Frequency Change ##
#############################
df <- read_table2(file="QTL_new_old_Class",col_names = TRUE,col_type = "dcccccc")
## split apart frequencies ##
freq <- matrix(unlist(strsplit(df$Freq, "_")), ncol = 16, byrow = TRUE)
freq <- apply(freq, 2, as.numeric)
## y axis is in terms of change in the favorable direction ##
## grab ones with a positive effect and subtract of initial value #
X <- which(df$Additive_Selective > 0)
freq[X, ] <- freq[X, ] - freq[X, 1]
## grab ones with a negative effect and subtract of initial value #
X <- which(df$Additive_Selective < 0)
freq[X, ] <- (freq[X, 1] - freq[X, ])
## get mean by generation
plotdf <- data.frame(cbind(c(0:15), colMeans(freq)))
names(plotdf) <- c("gen", "freq")

ggplot(plotdf, aes(x = gen, y = freq)) + geom_line(size = 1.0) + ggtitle("Favorable Allele Frequency Change") + theme_bw() +
  theme(plot.title = element_text(hjust = 0.5)) + ylab("Change in allele frequency since Genertion 0 ") +
  xlab("Generation")