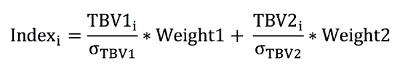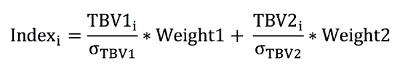Index True Breeding Value Selection


  The parameter file outlined below illustrates how to simulate a population undergoing selection based on an index value, which is comprised of the TBV for trait 1 and 2. The weight in the final index for trait 1 and 2 is 0.25 and 0.75, respectively. In order to make each trait have the same variance, each value is scaled by the standard deviation in the true breeding values for individuals born in the generation prior to when selection begins (e.g. Generation 3). The index for animal `i' is calculated as follows:

−−−−−−−| Running the Program Example |−−−−−−−
−| General |−
START: founder
SEED: 1500
−| Genome & Marker |−
CHR: 3
CHR_LENGTH: 150 150 150
NUM_MARK: 4000 4000 4000
QTL: 150 150 150
−| Population |−
FOUNDER_Effective_Size: Ne70
MALE_FEMALE_FOUNDER: 50 400 random 3
VARIANCE_A: 0.35 0.40 0.35
−| Selection |−
GENERATIONS: 15
INDIVIDUALS: 50 0.2 400 0.2
PROGENY: 1
SELECTION: index_tbv high
INDEX_PROPORTIONS: 0.25 0.75
CULLING: index_tbv 5
-| Mating |-
MATING: random125 simu_anneal

Parameter File Summary
  Sequence information is generated for three chromosomes with a length of 150 Megabases. The genome simulated has a high degree of short-range LD (Ne70). The SNP panel contains 12,000 markers (i.e. 4,000 markers per chromosome). For each chromosome, 150 randomly placed QTL and zero FTL mutations were generated. Across both quantitative traits simulated, a narrow sense heritability of 0.35 and only additive effects was generated (i.e. no dominance). The residual variance across both traits is 0.65. The two traits are simulated with a correlation of 0.40 and 0.00 for the additive genetic and residual environmental effects between trait 1 and trait 2. The founder population consisted of 50 males and 400 females. For each generation, a total of 50 males and 400 females are in the population. Random selecton of progeny and culling of parents was conducted for 3 generations. A total of 10 and 80 (0.2 replacement rate) male and female parents, respectively, are culled and replaced by new progeny each generation. After 3 generations, animals with a high index true breeding value were selected or culled each generation. The weight in the final index for trait 1 and 2 is 0.25 and 0.75, respectively. Fifteen generations were simulated. Each mating pair produced one progeny. Parents that had pedigree-based relationships greater than 0.125 were avoided, and this was optimized based on the simulated annealing method.

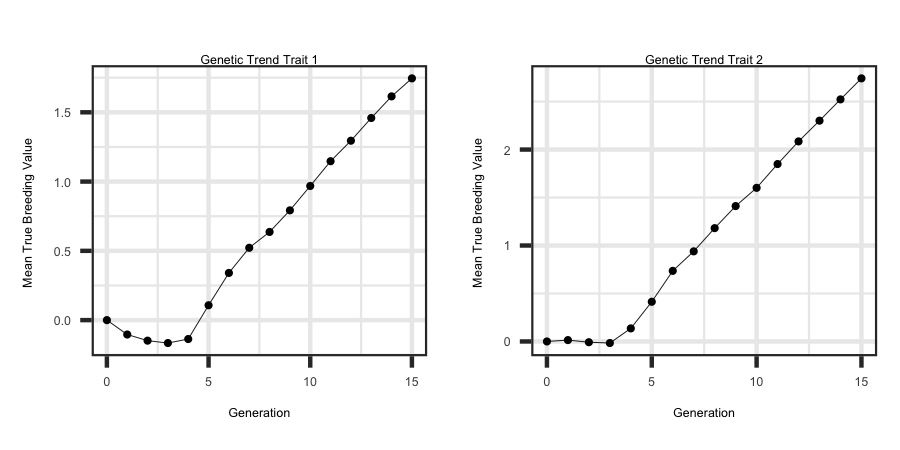
  Utilizing the R code outlined below the following plots were generated from the output files to see the response across both traits.

R-Code
rm(list = ls()); gc()
library(ggplot2); library(tidyverse)
## Change
setwd("/Users/jeremyhoward/Desktop/C++Code/18_GenoDiver_V3/GenoDiverFiles/")
#############################
## Plot True Genetic Value ##
#############################
df <- read_table2(file="Summary_Statistics_DataFrame_Performance",col_names = TRUE,col_type = "dccccccccccccc") %>%
  mutate(tbv1 = as.numeric(matrix(unlist(strsplit(tbv1, "[()]")), ncol = 2, byrow = TRUE)[, 1]),
               tbv2 = as.numeric(matrix(unlist(strsplit(tbv2, "[()]")), ncol = 2, byrow = TRUE)[, 1])) %>%
  select(Generation,tbv1,tbv2)

ggplot(df, aes(x = Generation, y = tbv1)) + geom_line(size = 1) + ggtitle("Genetic Trend Trait 1") + theme_bw() +
  theme(plot.title = element_text(hjust = 0.5)) + ylab("Mean True Breeding Value ")

ggplot(df, aes(x = Generation, y = tbv2)) + geom_line(size = 1) + ggtitle("Genetic Trend Trait 2") + theme_bw() +
 theme(plot.title = element_text(hjust = 0.5)) + ylab("Mean True Breeding Value ")